Convection-Diffusion-Reaction
Here, we discuss the discretization of the equation
We assume that \(\phi\) is discretized by cell-centered averages (note that cell centers may lie inside solid boundaries), and use finite volume methods to construct fluxes in a cut-cells and regular cells. Here, \(\mathbf{v}\) indicates a drift velocity and \(D\) is the diffusion coefficient.
Note
Using cell-centered versions \(\phi\) might be problematic for some models since the state is extended outside the valid region. Models might have to recenter the state in order compute e.g. physically meaningful reaction terms in cut-cells.
Source code for the convection-diffusion-reaction solvers reside in $DISCHARGE_HOME/Source/ConvectionDiffusionReaction and the full API can be found at https://chombo-discharge.github.io/chombo-discharge/doxygen/html/classCdrSolver.html.
CdrSolver
The CdrSolver class contains the interface for solving advection-diffusion-reaction problems.
CdrSolver is an abstract class and does not contain any specific advective or diffusive discretization (these are added by implementation classes).
Currently, the implementation layers consist of the following:
CdrMultigrid, which inherits from
CdrSolverand adds a second order accurate discretization for the diffusion operator.CdrCTU and CdrGodunov which inherit from
CdrMultigridand add a second order accurate spatial discretization for the advection operator.
Currently, we mostly use the CTU class which contains a second order accurate discretization with slope limiters.
CdrGodunov is a similar operator, but the advection code for this is distributed by the Chombo team.
The C++ API for these classes can be obtained from https://chombo-discharge.github.io/chombo-discharge/doxygen/html/classCdrSolver.html.
The advance methods for CdrSolver are encapsulated by the following functions:
// For advancing the diffusion equation with an implicit Euler method.
void advanceEuler(EBAMRCellData& a_newPhi, const EBAMRCellData& a_oldPhi, const EBAMRCellData& a_source, const Real a_dt) = 0;
// For advancing the diffusion equation with a Crank-Nicholson method.
void advanceCrankNicholson(EBAMRCellData& a_newPhi, const EBAMRCellData& a_oldPhi, const EBAMRCellData& a_source, const Real a_dt) = 0;
// For computing div(v*phi - D*grad(phi)).
void computeDivJ(EBAMRCellData& a_divJ, EBAMRCellData& a_phi, const Real a_dt, const bool a_conservativeOnly, const bool a_ebFlux, const bool a_domainFlux) = 0;
// For computing div(v*phi).
void computeDivF(EBAMRCellData& a_divJ, EBAMRCellData& a_phi, const Real a_dt, const bool a_conservativeOnly, const bool a_ebFlux, const bool a_domainFlux) = 0;
// For computing div(D*grad(phi)).
void computeDivD(EBAMRCellData& a_divJ, EBAMRCellData& a_phi, const Real a_dt, const bool a_conservativeOnly, const bool a_ebFlux, const bool a_domainFlux) = 0;
Discretization details
Explicit divergences and redistribution
Computing explicit divergences for equations like
is problematic because of the arbitarily small volume fractions of cut cells. In general, we seek a method-of-lines update \(\phi^{k+1} = \phi^k - \Delta t \left[\nabla\cdot \mathbf{G}^k\right]\) where \(\left[\nabla\cdot\mathbf{G}\right]\) is a stable numerical approximation based on some finite volume approximation.
Pure finite volume methods use
where \(\kappa\) is the volume fraction of a grid cell, \(\textrm{DIM}\) is the spatial dimension and the volume integral is written as discretized surface integral
The sum runs over all cell edges (faces in 3D) of the cell where \(G_f\) is the flux on the edge centroid and \(\alpha_f\) is the edge (face) aperture.
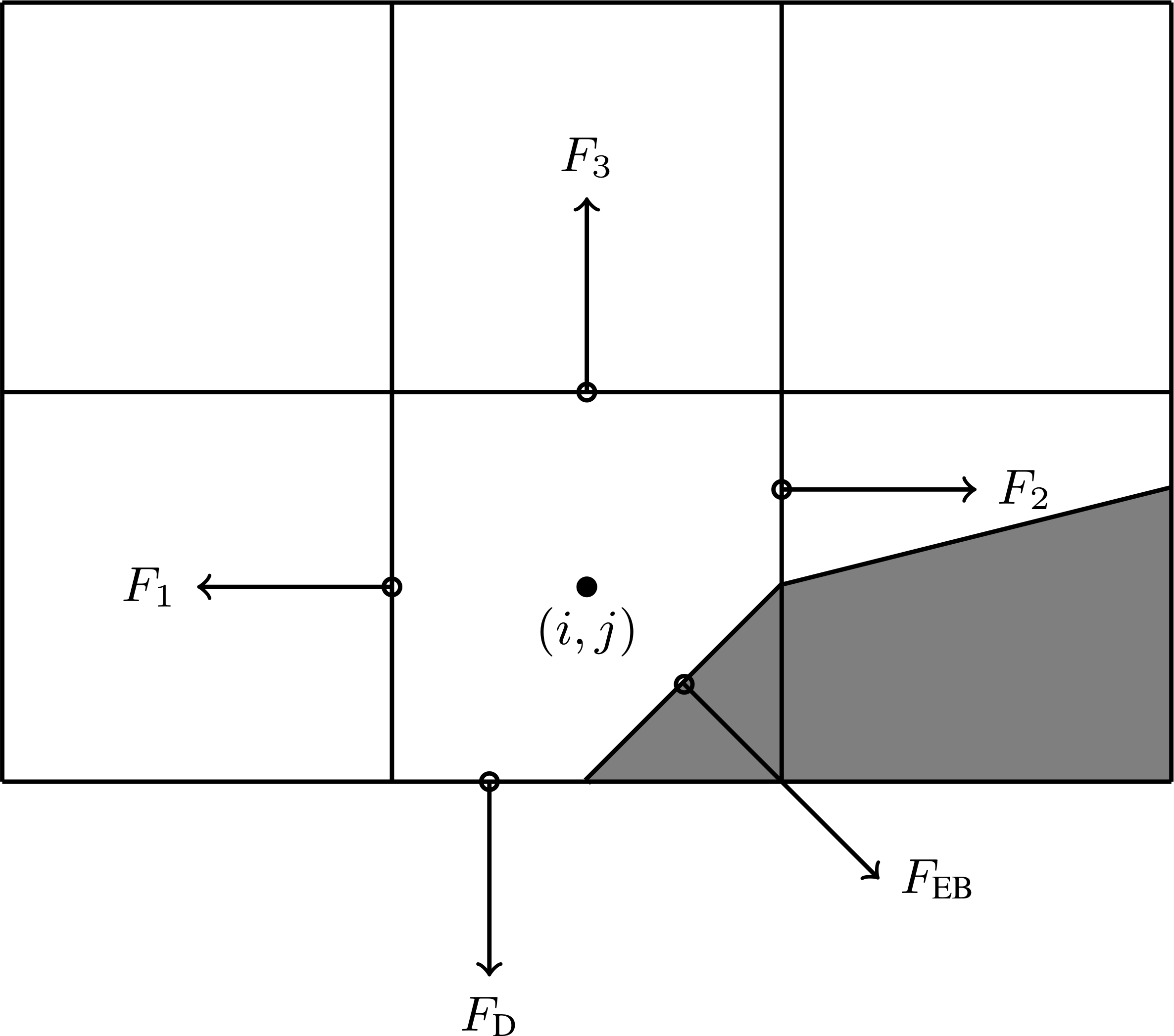
Fig. 22 Location of centroid fluxes for cut cells.
However, taking \([\nabla\cdot\mathbf{G}^k]\) to be this sum leads to a time step constraint proportional to \(\kappa\), which can be arbitrarily small. This leads to an unacceptable time step constraint for Eq. 2. We use the Chombo approach and expand the range of influence of the cut cells in order to stabilize the discretization and allow the use of a normal time step constraint. First, we compute the conservative divergence
where \(G_f = \mathbf{G}_f\cdot \mathbf{n}_f\). Next, we compute a non-conservative divergence \(D_{\mathbf{i}}^{nc}\)
where \(N(\mathbf{i})\) indicates some neighborhood of cells around cell \(\mathbf{i}\). Next, we compute a hybridization of the divergences,
and perform an intermediate update
The hybrid divergence update fails to conserve mass by an amount \(\delta M_{\mathbf{i}} = \kappa_{\mathbf{i}}\left(1-\kappa_{\mathbf{i}}\right)\left(D_{\mathbf{i}}^c - D_{\mathbf{i}}^{nc}\right)\). In order to main overall conservation, the excess mass is redistributed into neighboring grid cells. Let \(\delta M_{\mathbf{i}, \mathbf{j}}\) be the redistributed mass from \(\mathbf{j}\) to \(\mathbf{i}\) where
This mass is used as a local correction in the vicinity of the cut cells, i.e.
where \(\delta M_{\mathbf{j}\in N(\mathbf{i}), \mathbf{i}}\) is the total mass redistributed to cell \(\mathbf{i}\) from the other cells. After these steps, we define
Numerically, the above steps for computing a conservative divergence of a one-component flux \(\mathbf{G}\) are implemented in the convection-diffusion-reaction solvers, which also respects boundary conditions (e.g. charge injection). The user will need to call the function
virtual void CdrSolver::computeDivG(EBAMRCellData& a_divG, EBAMRFluxData& a_G, const EBAMRIVData& a_ebG)
where a_G is the numerical representation of \(\mathbf{G}\) over the cut-cell AMR hierarchy and must be stored on cell-centered faces, and a_ebG is the flux on the embedded boundary.
The above steps are performed by interpolating a_G to face centroids in the cut cells for computing the conservative divergence, and the remaining steps are then performed successively.
The result is put in a_divG.
Note that when refinement boundaries intersect with embedded boundaries, the redistribution process is far more complicated since it needs to account for mass that moves over refinement boundaries.
These additional complicated are taken care of inside a_divG, but are not discussed in detail here.
Caution
Mass redistribution has the effect of not being monotone and thus not TVD, and the discretization order is formally \(\mathcal{O}(\Delta x)\).
Explicit advection
Scalar advection updates follows the computation of the explicit divergence discussed in Explicit divergences and redistribution. The face-centered fluxes \(\mathbf{G} = \phi\mathbf{v}\) are computed by instantiation classes for the convection-diffusion-reaction solvers. The function signature for explicit advection is
void computeDivF(EBAMRCellData& a_divF, const EBAMRCellData& a_state, const Real a_dt);
where the face-centered fluxes are computed by using the velocities and boundary conditions that reside in the solver, and result is put in a_divF using the procedure outlined above.
The argument a_dt is the time step size.
It is not needed in a method-of-lines context, but it is used in e.g. CdrCTU for computing transverse derivatives in order to expand the stability region (i.e., use larger CFL numbers).
For example, in order to perform an advective advance over a time step \(\Delta t\), one would perform the following:
CdrSolver* solver;
const Real dt = 1.0;
EBAMRCellData& phi = solver->getPhi(); // Cell-centered state
EBAMRCellData& divF = solver->getScratch(); // Scratch storage in solver
solver->computeDivF(divF, phi, 0.0); // Computes divF
DataOps:incr(phi, divF, -dt); // makes phi -> phi - dt*divF
Explicit diffusion
Explicit diffusion is performed in much the same way as implicit advection, with the exception that the general flux \(\mathbf{G} = D\nabla\phi\) is computed by using centered differences on face centers. The function signature for explicit diffusion is
void computeDivD(EBAMRCellData& a_divF, const EBAMRCellData& a_state);
and we increment in the same way as for explicit advection:
CdrSolver* solver;
const Real dt = 1.0;
EBAMRCellData& phi = solver->getPhi(); // Cell-centered state
EBAMRCellData& divD = solver->getScratch(); // Scratch storage in solver
solver->computeDivF(divD, phi, 0.0); // Computes divD
DataOps:incr(phi, divD, dt); // makes phi -> phi + dt*divD
Explicit advection-diffusion
There is also functionality for aggregating explicit advection and diffusion advances. The reason for this is that the cut-cell overhead is only applied once on the combined flux \(\phi\mathbf{v} - D\nabla\phi\) rather than on the individual fluxes. For non-split methods this leads to some performance improvement since the interpolation of fluxes on cut-cell faces only needs to be performed once. The signature for this is precisely the same as for explicit advection only:
void computeDivJ(EBAMRCellData& a_divJ, const EBAMRCellData& a_state, const Real a_extrapDt)
where the face-centered fluxes are computed by using the velocities and boundary conditions that reside in the solver, and result is put in a_divF.
For example, in order to perform an advective advance over a time step \(\Delta t\), one would perform the following:
const Real dt = 1.0;
EBAMRCellData& phi = solver->getPhi(); // Cell-centered state
EBAMRCellData& divJ = solver->getScratch(); // Scratch storage in solver
solver->computeDivJ(divJ, phi, 0.0); // Computes divD
DataOps:incr(phi, divJ, -dt); // makes phi -> phi - dt*divJ
Often, time integrators have the option of using implicit or explicit diffusion.
If the time-evolution is not split (i.e. not using a Strang or Godunov splitting), the integrators will often call computeDivJ rather separately calling computeDivF and computeDivD.
If you had a split-step Godunov method, the above procedure for a forward Euler method for both parts would be:
CdrSolver* solver;
const Real dt = 1.0;
solver->computeDivF(divF, phi, 0.0); // Computes divF = div(n*phi)
DataOps:incr(phi, divF, -dt); // makes phi -> phi - dt*divF
solver->computeDivD(divD, phi); // Computes divD = div(D*nabla(phi))
DataOps:incr(phi, divD, dt); // makes phi -> phi + dt*divD
However, the cut-cell redistribution dance (flux interpolation, hybrid divergence, and redistribution) would be performed twice.
Implicit diffusion
Implicit diffusion can occasionally be necesasry. The convection-diffusion-reaction solvers support two basic diffusion solves: Backward Euler and the Crank-Nicholson methods. The function signatures for these are
void advanceEuler(EBAMRCellData& a_newPhi, const EBAMRCellData& a_oldPhi, const EBAMRCellData& a_source, const Real a_dt) = 0;
void advanceCrankNicholson(EBAMRCellData& a_newPhi, const EBAMRCellData& a_oldPhi, const EBAMRCellData& a_source, const Real a_dt) = 0;
where a_newPhi is the state at the new time \(t + \Delta t\), a_oldPhi is the state at time \(t\) and a_source is the source term which strictly speaking should be centered at time \(t + \Delta t\) for the Euler update and at time \(t + \Delta t/2\) for the Crank-Nicholson update.
This may or may not be possible for your particular problem.
For example, performing a split step Godunov method for advection-diffusion is as simple as:
// First. Compute phi = phi - dt*div(F)
solver->computeDivF(divF, phi, 0.0);
DataOps:incr(phi, divF, -dt);
// Implicit diffusion advance over a time step dt
DataOps::copy(phiOld, phi);
solver->advanceEuler(phi, phiOld, dt);
CdrMultigrid
CdrMultigrid adds second-order accurate implicit diffusion code to CdrSolver, but leaves the advection code unimplemented.
The class can use either implicit or explicit diffusion using second-order cell-centered stencils.
In addition, CdrMultigrid adds two implicit time-integrators, an implicit Euler method and a Crank-Nicholson method.
The CdrMultigrid layer uses the Helmholtz discretization discussed in Helmholtz equation.
It implements the pure functions required by CdrSolver but introduces a new pure function
virtual void advectToFaces(EBAMRFluxData& a_facePhi, const EBAMRCellData& a_phi, const Real a_dt) = 0;
The faces states defined by the above function are used when forming a finite-volume approximation to the divergence operators, see Discretization details.
CdrCTU
CdrCTU is an implementation class that uses the corner transport upwind (CTU) discretization.
The CTU discretization uses information that propagates over corners of grid cells when calculating the face states.
It can combine this with use various limiters:
No limiter (pure CTU)
Minmod
Superbee
Monotonized central differences
In addition, CdrCTU can turn off the transverse terms in which case the discretization reduces to the donor cell method.
Our motivation for using the CTU discretization lies in the time step selection for the CTU and donor-cell methods, see Time step limitation.
Typically, we want to achieve a dimensionally independent time step that is the same in 1D, 2D, and 3D, but without directional splitting.
Face extrapolation
The finite volume discretization uses an upstream-centered Taylor expansion that extrapolates the cell-centered term to half-edges and half-steps:
Note that the truncation order is \(\Delta t^2 + \Delta x\Delta t\) where the latter term is due to the cross-derivative \(\frac{\partial^2\phi}{\partial t\partial x}\). The resulting expression in 2D for a velocity field \(\mathbf{v} = (u,v)\) is
Here, \(\Delta^x\) are the regular (normal) slopes whereas \(\Delta^y\) are the transverse slopes. The transverse slopes are given by
Slopes
For the normal slopes, the user can choose between the minmod, superbee, and monotonized central difference (MC) slopes. Let \(\Delta_l = \phi_{i,j}^n - \phi_{i-1,j}^n\) and \(\Delta_r = \phi_{i+1,j}^n - \phi_{i,j}^n\). The slopes are given by:
where for the superbee slope we have \(\Delta_1 = \text{minmod}\left(\Delta_l, 2\Delta_r\right)\) and \(\Delta_2 = \text{minmod}\left(\Delta_r, 2\Delta_l\right)\).
Note
When using slopes, monotonicity is not guaranteed for the CTU discretization. If slopes are turned off, however, the scheme is guaranteed to be monotone.
Time step limitation
The stability region for the donor-cell and corner transport upwind methods are:
Note that when the flow is diagonal to the grid, i.e. \(|v_x| = |v_y| = |v_z|\), the CTU can use a time step that is three times larger than for the donor-cell method.
Class options
When running the CdrCTU solver the user can adjust the advective algorithm by turning on/off slope limiters and the transverse term through the class options:
CdrCTU.slope_limiter, which must be none, minmod, mc, or superbee.CdrCTU.use_ctu, which must be true or false.
If the transverse terms are turned off, CdrCTU will compute the donor-cell time step.
CdrGodunov
CdrGodunov inherits from CdrMultigrid and adds advection code for Godunov methods.
This class borrows from Chombo internals (specifically, EBLevelAdvectIntegrator) and can do second-order advection with time-extrapolation.
CdrGodunov supplies (almost) the same discretization as CdrCTU with the exception that the underlying discretization can also be used for the incompressible Navier-Stokes equation.
However, it only supports the monotonized central difference limiter.
Caution
CdrGodunov will be removed from future versions of chombo-discharge.
Using CdrSolver
Setting up the solver
To set up the CdrSolver, the following commands are usually sufficient:
// Assume m_solver and m_species are pointers to a CdrSolver and CdrSpecies
auto solver = RefCountedPtr<CdrSolver> (new MyCdrSolver());
auto species = RefCountedPtr<CdrSpecies> (new MyCdrSpecies());
To see an example, the advection-diffusion code in /Physics/AdvectionDiffusion/CD_AdvectionDiffusionStepper.cpp shows how to set up a CdrSolver.
Filling the solver
In order to obtain mesh data from the CdrSolver, the user should use the following public member functions:
EBAMRCellData& getPhi(); // Return phi
EBAMRCellData& getSource(); // Returns S
EBAMRCellData& getCellCenteredVelocity(); // Get cell-centered velocity
EBAMRFluxData& getFaceCenteredDiffusionCoefficient(); // Returns D
EBAMRIVData& getEbFlux(); // Returns flux at EB
EBAMRIFData& getDomainFlux(); // Returns flux at domain boundaries
To set the drift velocities, the user will fill the cell-centered velocities.
Interpolation to face-centered transport fluxes are done by CdrSolver during the discretization step.
The general way of setting the velocity is to get a direct handle to the velocity data:
CdrSolver solver;
EBAMRCellData& veloCell = solver.getCellCenteredVelocity();
Then, veloCell can be filled with the cell-centered velocity.
This would typically look something like this:
EBAMRCellData& veloCell = m_solver->getCellCenteredVelocity();
for (int lvl = 0; lvl <= m_amr->getFinestLevel(); lvl++){
const DisjointBoxLayout& dbl = m_amr->getGrids()[lvl];
for (DataIterator dit(dbl); dit.ok(); ++dit){
EBCellFAB& patchVel = (*veloCell[lvl])[dit()];
// Do something with patchVel
}
}
The same procedure goes for the source terms, diffusion coefficients, boundary conditions and so on. For example, an explicit Euler discretization for the problem \(\partial_t\phi = S\) is:
CdrSolver* solver;
const Real dt = 1.0;
EBAMRCellData& phi = solver->getPhi();
EBAMRCellData& src = solver->getSource();
DataOps::incr(phi, src, dt);
Adjusting output
It is possible to adjust solver output when plotting data.
This is done through the input file for the class that you’re using.
For example, for the CdrCTU implementation the following variables are available:
CdrCTU.plt_vars = phi vel src dco ebflux # Plot variables. Options are 'phi', 'vel', 'dco', 'src'
Here, you adjust the plotted variables by adding or omitting them from your input script. E.g. if you only want to plot the cell-centered states you would do:
CdrGodunov.plt_vars = phi # Plot variables. Options are 'phi', 'vel', 'dco', 'src', 'ebflux'
CdrSpecies
The CdrSpecies class is a supporting class that passes information and initial conditions into CdrSolver instances.
CdrSpecies specifies whether or not the advect-diffusion solver will use only advection, diffusion, both advection and diffusion, or neither.
It also specifies initial data, and provides a string identifier to the class (e.g. for identifying output in plot files).
However, it does not contain any discretization.
Note
Click here for the CdrSpecies C++ API.
The below code block shows an example of how to instantiate a species. Here, diffusion code is turned off and the initial data is one everywhere.
class MySpecies : public CdrSpecies{
public:
MySpecies(){
m_mobile = true;
m_diffusive = false;
m_name = "mySpecies";
}
~MySpecies() = default;
Real initialData(const RealVect a_pos, const Real a_time) const override {
return 1.0;
}
}
Tip
It is also possible to use computational particles as an initial condition in CdrSpecies.
In this case you need to fill m_initialParticles, and these are then deposited with a nearest-grid-point scheme when instantiating the solver.
See Particles for further details.
Example application(s)
Example applications that use the CdrSolver are: