Electrostatics model

The electrostatics model solves

\[\nabla\cdot\left(\epsilon_r\nabla\Phi\right) = -\frac{\rho}{\epsilon_0}\]

subject to the constraints and boundary conditions given in FieldSolver.

There is currently no CellTagger implementation for this module, so AMR support is restricted to refinement based on geometric criteria. The full implementation for this model consists only of the following class:

• FieldStepper, which implements TimeStepper.

Tip

The source for this module is found in $DISCHARGE_HOME/Physics/Electrostatics. The C++ API is found here.

Time stepping

FieldStepper is a class with only stationary solves. This is enforced by making the TimeStepper::advance method throw an error, while the field solve itself is done in the initialization procedure in TimeStepper::postInitialize.

Warning

To run the solver, one must set Driver.max_steps = 0.

Setting the space charge

Default behavior

By default, the initial space charge for this problem is given by a Gaussian

\[\rho\left(\mathbf{x}\right) = \rho_0\exp\left(-\frac{\left|\mathbf{x}-\mathbf{x}_0\right|^2}{2R^2}\right),\]

where \(\rho_0\) is an amplitude, \(\mathbf{x}_0\) is the center and \(R\) is the Gaussian radius. These are set through respective configuration options, see Solver configuration.

For a more general way of specifying the space charge, FieldStepper has a public member function

/*!
  @brief Set space charge
  @param[in] a_rho Space charge distribution
*/
void
setRho(const std::function<Real(const RealVect& a_pos)>& a_rho, const phase::which_phase a_phase) noexcept;

Setting the surface charge

By default, the initial surface charge is set to a constant, see Solver configuration. For a more general way of specifying the surface charge, FieldStepper has a public member function

/*!
  @brief Set surface charge
  @param[in] a_sigma Surface charge distribution
*/
void
setSigma(const std::function<Real(const RealVect& a_pos)>& a_sigma) noexcept;

Solver configuration

The FieldStepper has relatively few configuration options, which are mostly limited to setting the space and surface charge The configuration options for FieldStepper are given below:

# ====================================================================================================
# FIELD_STEPPER CLASS OPTIONS
# ====================================================================================================
FieldStepper.verbosity        = -1        ## Verbosity
FieldStepper.realm            = primal    ## Realm where solver lives.
FieldStepper.load_balance     = false     ## Load balance or not.
FieldStepper.box_sorting      = morton    ## If you load balance you can redo the box sorting.
FieldStepper.init_sigma       = 0.0       ## Surface charge density
FieldStepper.init_rho         = 0.0       ## Space charge density (value)
FieldStepper.rho_center       = 0 0 0     ## Space charge blob center
FieldStepper.rho_radius       = 1.0       ## Space charge blob radius

Important

Setup of boundary conditions is not a job for FieldStepper, but occurs through the respective ComputationalGeometry and FieldSolver.

Setting up a new problem

To set up a new problem, using the Python setup tools in $DISCHARGE_HOME/Physics/Electrostatics is the simplest way. A full description is available in the README.md contained in the folder:

# Physics/Electrostatics
This physics module runs one of the electrostatic field solvers.
It does not feature mesh refinement, but this is possible to implement by adding a CellTagger to the module. 

The source files consist of the following:

* **CD_FieldStepper.H/cpp** Implementation of TimeStepper, for solving the Poisson equation. 

## Setting up a new application
To set up a new problem, use the Python script. For example:

```shell
python setup.py -base_dir=/home/foo/MyApplications -app_name=MyElectrostatics -geometry=Vessel
```

To install within chombo-discharge:

```shell
python setup.py -base_dir=$DISCHARGE_HOME/MyApplications -app_name=MyElectrostatics -geometry=Vessel
```

The application will be installed to $DISCHARGE_HOME/MyApplications/MyElectrostatics.
The user will need to modify the geometry and set the initial conditions through the inputs file. 

## Modifying the application
Users are free to modify this application, e.g. adding support for mesh refinement or setting up more complex boundary conditions. 

To see available setup options, use

python setup.py --help

Example programs

Some example programs for this module are given in

• $DISCHARGE_HOME/Exec/Examples/Electrostatics/Armadillo

• $DISCHARGE_HOME/Exec/Examples/Electrostatics/Mechshaft

• $DISCHARGE_HOME/Exec/Examples/Electrostatics/ProfiledSurface

Verification

Spatial convergence tests for this module (and consequently the underlying numerical discretization) are given in

• $DISCHARGE_HOME/Exec/Convergence/Electrostatics/C1

• $DISCHARGE_HOME/Exec/Convergence/Electrostatics/C2

• $DISCHARGE_HOME/Exec/Convergence/Electrostatics/C3

All tests operate by computing solutions on grids with resolutions \(\Delta x\) and \(\Delta x/2\) and then computing the solution error using the approach outlined in Spatial convergence.

C1: Coaxial cable

$DISCHARGE_HOME/Exec/Convergence/Electrostatics/C1 is a spatial convergence test in a coaxial cable geometry. Figure Fig. 28 shows the field distribution. Note that there is a dielectric embedded between the two cylindrical shells.

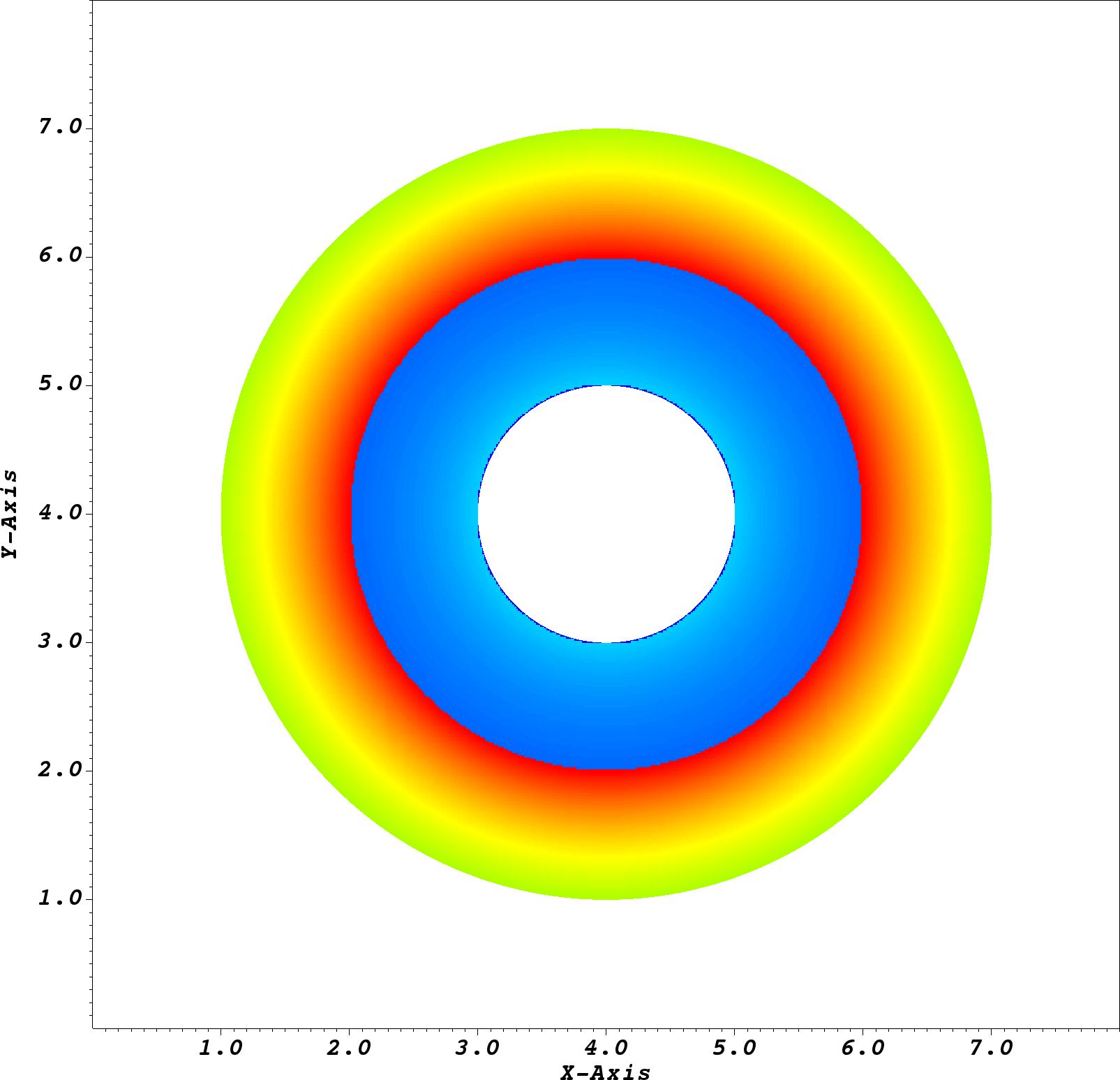
Fig. 28 Field distribution for a coaxial cable geometry on a \(512^2\) grid.

The computed convergence rates are given in Fig. 29. We find second order convergence in all three norms.

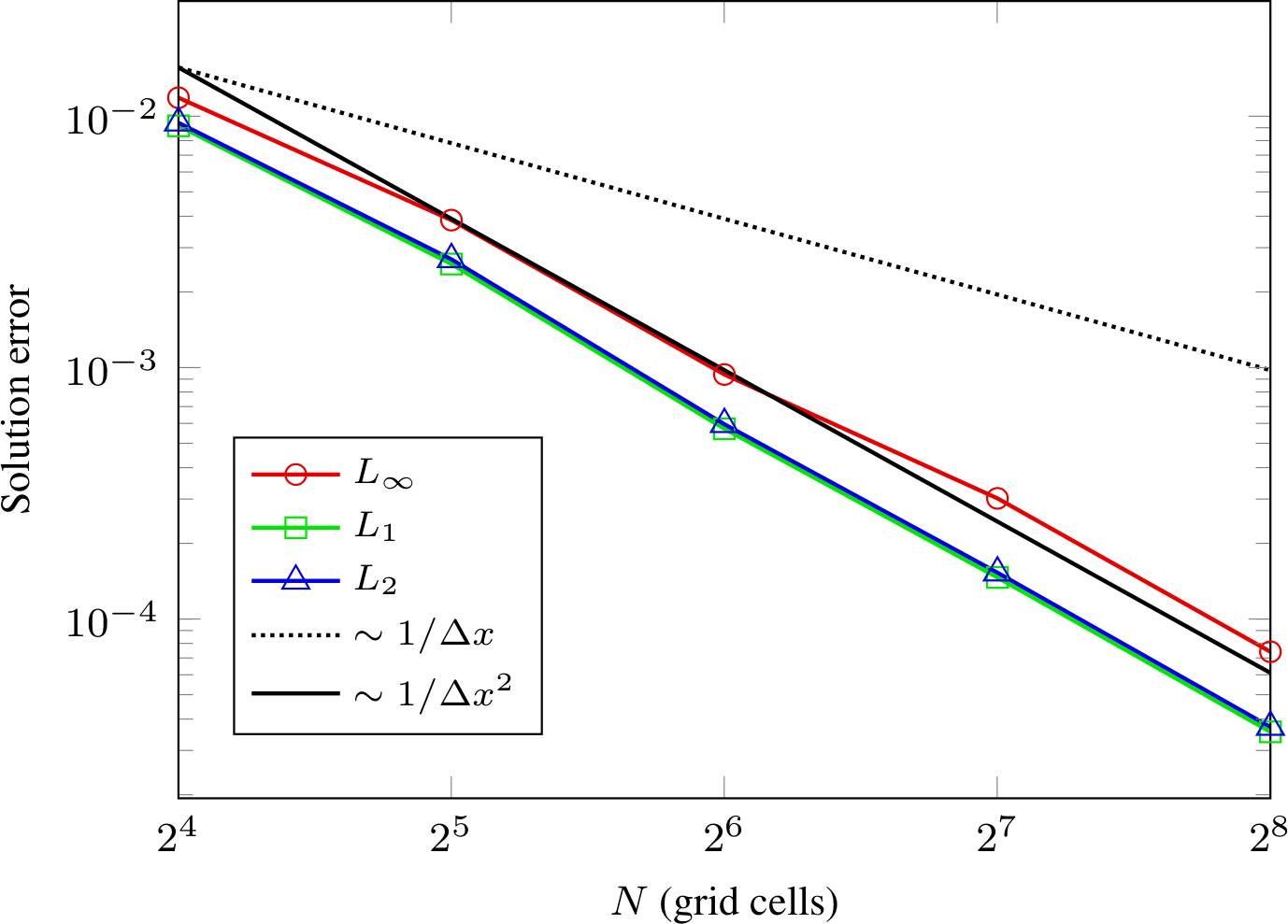
Fig. 29 Spatial convergence rates for two-dimensional coaxial cable geometry.

C2: Profiled surface

$DISCHARGE_HOME/Exec/Convergence/Electrostatics/C2 is a 2D spatial convergence test for an electrode and a dielectric slab with surface profiles. Figure Fig. 30 shows the field distribution.

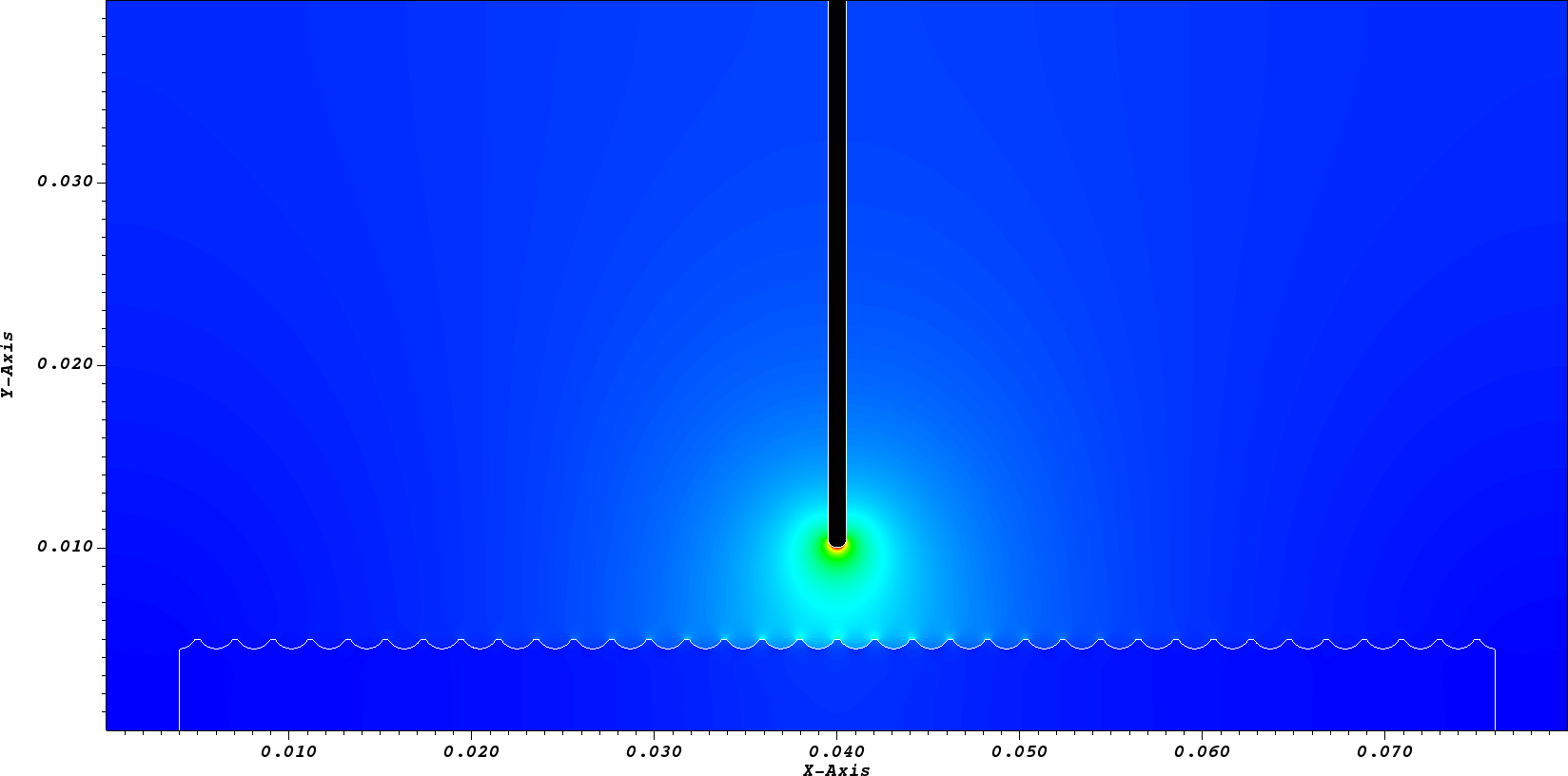
Fig. 30 Field distribution for a profiled surface geometry on a \(2048^2\) grid.

The computed convergence rates are given in Fig. 31. We find second order convergence in all three norms.

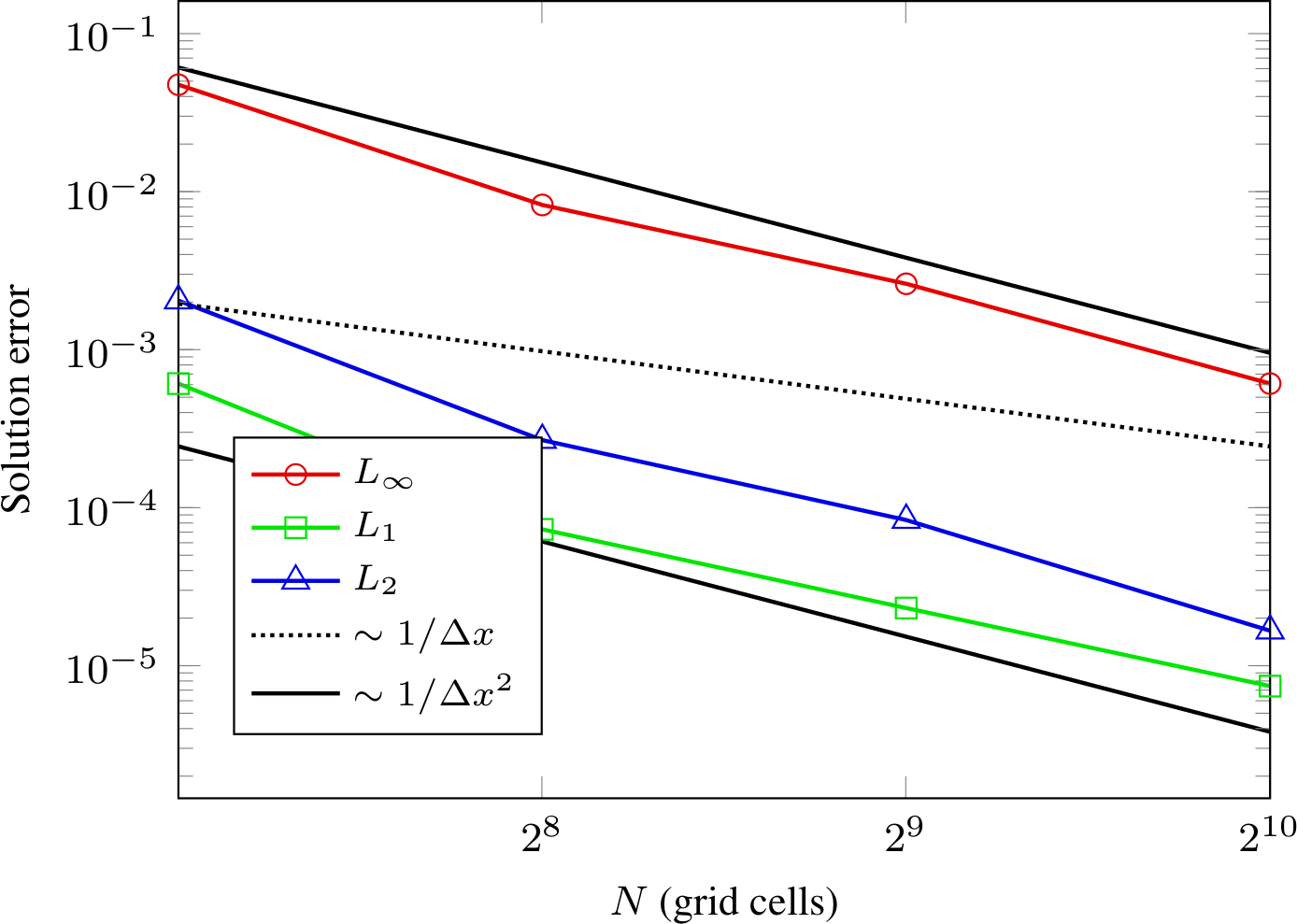
Fig. 31 Spatial convergence rates for two-dimensional dielectric surface profile.

C3: Dielectric shaft

$DISCHARGE_HOME/Exec/Convergence/Electrostatics/C3 is a 3D spatial convergence test for a dielectric shaft perpendicular to the background field. Figure Fig. 32 shows the field distribution for a \(256^3\) grid.

Fig. 32 Field distribution for a profiled surface geometry on a \(256^3\) grid.

The computed convergence rates are given in Fig. 33. We find second order convergence in \(L_1\) and \(L_2\) on all grids, and find second order convergence in the max-norm on sufficiently fine grids. On coarser grids, the reduced convergence rate in the max-norm is probably due to under-resolution of the geometry.

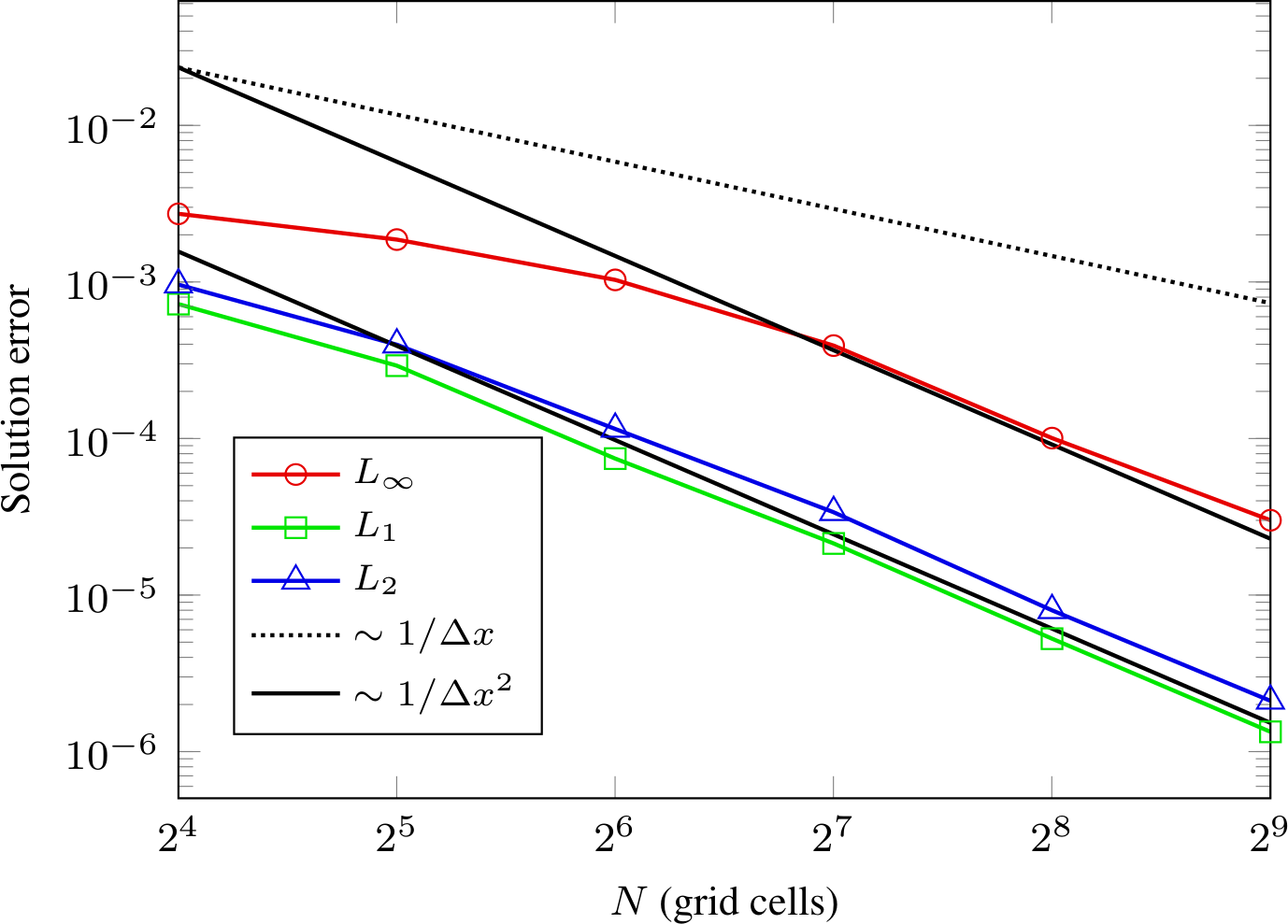
Fig. 33 Spatial convergence rates.