Advection-diffusion model

The advection-diffusion model simply advects a scalar quantity with EB and AMR. The equation of motion is

\[\frac{\partial\phi}{\partial t} + \nabla\cdot\left(\mathbf{v}\phi - D\nabla\phi\right) = 0.\]

The full implementation for this model consists of the following classes:

  • AdvectionDiffusionStepper, which implements TimeStepper.

  • AdvectionDiffusionSpecies, which implements CdrSpecies, and thus sparses the initial condition into the problem.

  • AdvectionDiffusionTagger, which implements CellTagger and flags cells for refinement and coarsening.

This module only uses CdrSolver.

Tip

The source code for this problem is found in $DISCHARGE_HOME/Physics/AdvectionDiffusion. See AdvectionDiffusionStepper for the C++ API for this time stepper.

Time stepping

Two time stepping algorithms are supported:

  1. A second-order Runge-Kutta method (Heun’s method).

  2. An implicit-explicit method (IMEX) which uses corner-transport upwind (CTU, see CdrCTU) and a Crank-Nicholson diffusion solve.

    Important

    The Crank-Nicholson method is known to be marginally stable.

See Solver configuration to see how to select between these two algorithms.

Heun’s method

For Heun’s method we perform the following steps: Let \(\left[\nabla\cdot\mathbf{J}\left(\phi\right)\right]\) be the finite-volume approximation to \(\nabla\cdot\left(\mathbf{v}\phi - D\nabla\phi\right)\), where \(\mathbf{J}\left(\phi\right) = \mathbf{v}\phi - D\nabla\phi\). The Runge-Kutta advance is then

\[\begin{split}\phi^\prime &= \phi^k - \Delta t\left[\nabla\cdot\mathbf{J}\left(\phi^k\right)\right]\\ \phi^{k+1} &= \phi^k - \frac{\Delta t}{2}\left(\left[\nabla\cdot\mathbf{J}\left(\phi^k\right)\right] + \left[\nabla\cdot\mathbf{J}\left(\phi^\prime\right)\right]\right)\end{split}\]

Warning

Note that when diffusion and advecting is coupled in this way, we do not include the transverse terms in the CdrCTU discretization and limit the time step by

\[\Delta t \leq \frac{1}{\frac{\sum_{i=1}^d |v_i|}{\Delta x} + \frac{2dD}{\Delta x^2}},\]

where \(d\) is the dimensionality and \(D\) is the diffusion coefficient.

IMEX

For the implicit-explicit advance, we use the CdrCTU discretization to center the divergence at the half time step. We seek the update

\[\frac{\phi^{k+1} - \phi^k}{\Delta t} - \frac{1}{2}\left[\nabla\left(D\nabla\phi^k\right) + \nabla\left(D\nabla\phi^{k+1}\right)\right] = -\nabla\cdot\mathbf{v}\phi^{k+1/2},\]

which is a Crank-Nicholson discretization of the diffusion equation with a source term centered on \(k+1/2\). We use the CdrCTU for obtaining the edge states \(\phi^{k+1/2}\) and then complete the update by solving the corresponding Helmholtz equation

\[\phi^{k+1} - \frac{\Delta t}{2}\nabla\left(D\nabla\phi^{k+1}\right) = \phi^k - \Delta t\nabla\cdot\mathbf{v}\phi^{k+1/2} + \frac{\Delta t}{2}\nabla\left(D\nabla\phi^k\right).\]

In this case the time step limitation is

\[\Delta t \leq \frac{\Delta x}{\sum_i\left|v_i\right|}.\]

Warning

It is possible to use this module with any implementation of CdrSolver, but the IMEX discretization only makes sense if the hyperbolic term can be centered on \(k+1/2\).

If the truncation order of \(\phi^{k+1/2}\) is \(\mathcal{O}\left(\Delta t^2\right)\), the resulting IMEX discretization is globally second order accurate. For the CdrCTU discretization the edge states are accurate to \(\mathcal{O}\left(\Delta t\Delta x\right)\), so the scheme is globally first order convergent (but with a small error constant).

Initial data

Default behavior

By default, the initial data for this problem is given by a super-Gaussian blob

\[\phi\left(\mathbf{x},t=0\right) = \phi_0\exp\left(-\frac{\left|\mathbf{x}-\mathbf{x}_0\right|^4}{2R^4}\right),\]

where \(\phi_0\) is an amplitude, \(\mathbf{x}_0\) is the blob center and \(R\) is the blob radius. These are set by the input options

AdvectionDiffusion.blob_amplitude     = 1.0      ## Blob amplitude
AdvectionDiffusion.blob_radius        = 0.1      ## Blob radius
AdvectionDiffusion.blob_center        = 0 0 0    ## Blob center

Custom value

For a more general way of specifying initial data, AdvectionDiffusionStepper has a public member function

/*!
  @brief Set the initial data..
  @param[in] a_initData Initial data function. 
*/
void
setInitialData(const std::function<Real(const RealVect& a_position)>& a_initData) noexcept;

Velocity field

Default behavior

The default velocity field for this class is

\[\begin{split}v_x &= -r\omega\sin\theta, \\ v_y &= r\omega\cos\theta, \\ v_z &= 0,\end{split}\]

where \(r = \sqrt{x^2 + y^2}\), \(\tan\theta = \frac{x}{y}\). I.e. the flow field is a circulation around the Cartesian grid origin.

To adjust the velocity field through \(\omega\), simply set the following option:

AdvectionDiffusion.omega              = 1.0      ## Rotation velocity

Custom value

For a more general way of setting a user-specified velocity, AdvectionDiffusionStepper has a public member function

/*!
  @brief Set the velocity field. 
  @param[in] a_velocity Velocity field. 
*/
void
setVelocity(const std::function<RealVect(const RealVect& a_position)>& a_velocity) noexcept;

Diffusion coefficient

Default behavior

The default diffusion coefficient for this problem is set to a constant. To adjust it, \(\omega\), set

AdvectionDiffusion.diffco             = 1.0      ## Diffusion coefficient

to a chosen value.

Custom value

For a more general way of setting the diffusion coefficient, AdvectionDiffusionStepper has a public member function

/*!
  @brief Set the diffusion coeffieint. 
  @param[in] a_diffusion Diffusion coefficient
*/
void
setDiffusionCoefficient(const std::function<Real(const RealVect& a_position)>& a_diffusion) noexcept;

Boundary conditions

At the EB, this module uses a wall boundary condition (i.e. no flux into or out of the EB). On domain edges (faces in 3D), the user can select between wall boundary conditions or outflow boundary conditions by selecting the corresponding input option for the solver. See CdrCTU.

Cell refinement

The cell refinement is based on two criteria:

  1. The amplitude of \(\phi\).

  2. The local curvature \(\left|\nabla\phi\right|\Delta x/\phi\).

We refine if the curvature is above some threshold \(\epsilon_1\) and the amplitude is above some threshold \(\epsilon_2\). These can be adjusted through

# Cell tagging controls
# ---------------------
AdvectionDiffusion.refine_curv     = 0.1     ## Refine if curvature exceeds this
AdvectionDiffusion.refine_magn     = 1E-2    ## Only tag if magnitude eceeds this
AdvectionDiffusion.buffer          = 0       ## Grow tagged cells

By default, every cell that fails to meet the above two criteria is coarsened.

Setting up a new problem

To set up a new problem, using the Python setup tools in $DISCHARGE_HOME/Physics/AdvectionDiffusion is the simplest way. A full description is available in the README.md contained in the folder:

# Physics/AdvectionDiffusion
This physics module solves for an advection-diffusion process of a single scalar quantity. This module contains files for setting up the initial conditions
and advected species, basic integrators, and a cell tagger for refining grid cells. 

The source files consist of the following:

* **CD_AdvectionDiffusionSpecies.H** Implementation of CdrSpecies, for setting up initial conditions and turning on/off advection and diffusion.
* **CD_AdvectionDiffusionTagger.H/cpp**  Implementation of CellTagger, for flagging cells for refinement and coarsening.
* **CD_AdvectionDiffusionStepper.H/cpp** Implementation of TimeStepper, for advancing the advection-diffusion equation. 

# Setting up a new problem
To set up a new problem, use the Python script. For example:

```shell
python setup.py -base_dir=/home/foo/MyApplications -app_name=MyAdvectionDiffusion -geometry=Vessel
```

To install within chombo-discharge:

```shell
python setup.py -base_dir=$DISCHARGE_HOME/MyApplications -app_name=MyAdvectionDiffusion -geometry=Vessel
```

The application will then be installed to $DISCHARGE_HOME/MyApplications/MyAdvectionDiffusion.
The user will need to modify the geometry and set the initial conditions through the inputs file.

To see available setup options, use

python setup.py --help

Solver configuration

The AdvectionDiffusionStepper and AdvectionDiffusionTagger classes come with user-configurable input options that can be adjusted at runtime. The configuration options for AdvectionDiffusionStepper are given below:

# ====================================================================================================
# AdvectionDiffusionStepper class options
# ====================================================================================================
AdvectionDiffusion.verbosity      = -1      ## Verbosity
AdvectionDiffusion.diffusion      = true    ## Turn on/off diffusion
AdvectionDiffusion.advection      = true    ## Turn on/off advection
AdvectionDiffusion.integrator     = imex    ## 'heun' or 'imex'

# Default velocity, diffusion, and initial data
# ---------------------------------------------
AdvectionDiffusion.blob_amplitude     = 1.0      ## Blob amplitude
AdvectionDiffusion.blob_radius        = 0.1      ## Blob radius
AdvectionDiffusion.blob_center        = 0 0 0    ## Blob center
AdvectionDiffusion.omega              = 1.0      ## Rotation velocity
AdvectionDiffusion.diffco             = 1.0      ## Diffusion coefficient

# Time step settings
# ------------------
AdvectionDiffusion.cfl        = 0.5      ## CFL number
AdvectionDiffusion.min_dt     = 0.0      ## Smallest acceptable time step
AdvectionDiffusion.max_dt     = 1.E99    ## Largest acceptable time step

# Cell tagging controls
# ---------------------
AdvectionDiffusion.refine_curv     = 0.1     ## Refine if curvature exceeds this
AdvectionDiffusion.refine_magn     = 1E-2    ## Only tag if magnitude eceeds this
AdvectionDiffusion.buffer          = 0       ## Grow tagged cells

Example programs

Some example programs for this module are given in

  • $DISCHARGE_HOME/Exec/Examples/AdvectionDiffusion/DiagonalFlowNoEB

  • $DISCHARGE_HOME/Exec/Examples/AdvectionDiffusion/PipeFlow

Verification

Spatial and temporal convergence tests for this module (and thus also the underlying solver implementation) are given in

  • $DISCHARGE_HOME/Exec/Convergence/AdvectionDiffusion/C1

  • $DISCHARGE_HOME/Exec/Convergence/AdvectionDiffusion/C2

C1: Spatial convergence

A spatial convergence test is given in $DISCHARGE_HOME/Exec/Convergence/AdvectionDiffusion/C1. The problem solves for an advected and diffused scalar in a rotational velocity in the presence of an EB:

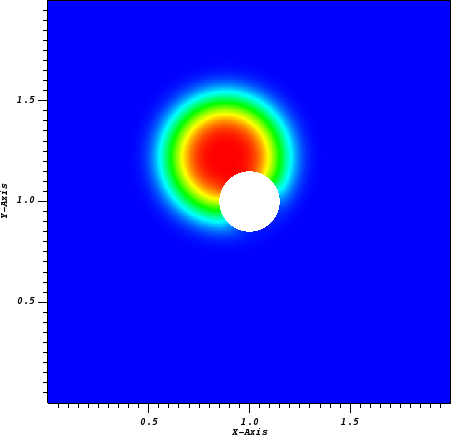
../_images/AdvectionDiffusionC1_1.png

Fig. 25 Final state on a \(512^2\) uniform grid.

To compute the convergence rate we compute two solutions with grid spacings \(\Delta x\) and \(\Delta x/2\), and estimate the solution error using the approach in Spatial convergence. Figure Fig. 26 shows the computed convergence rates with various choice of slope limiters. We find 2nd order convergence in all three norms for sufficiently fine grid when using slope limiters, and first order convergence when limiters are turned off. The reduced convergence rates at coarser grids occur due to 1) insufficient resolution of the initial density profile and 2) under-resolution of the geometry.

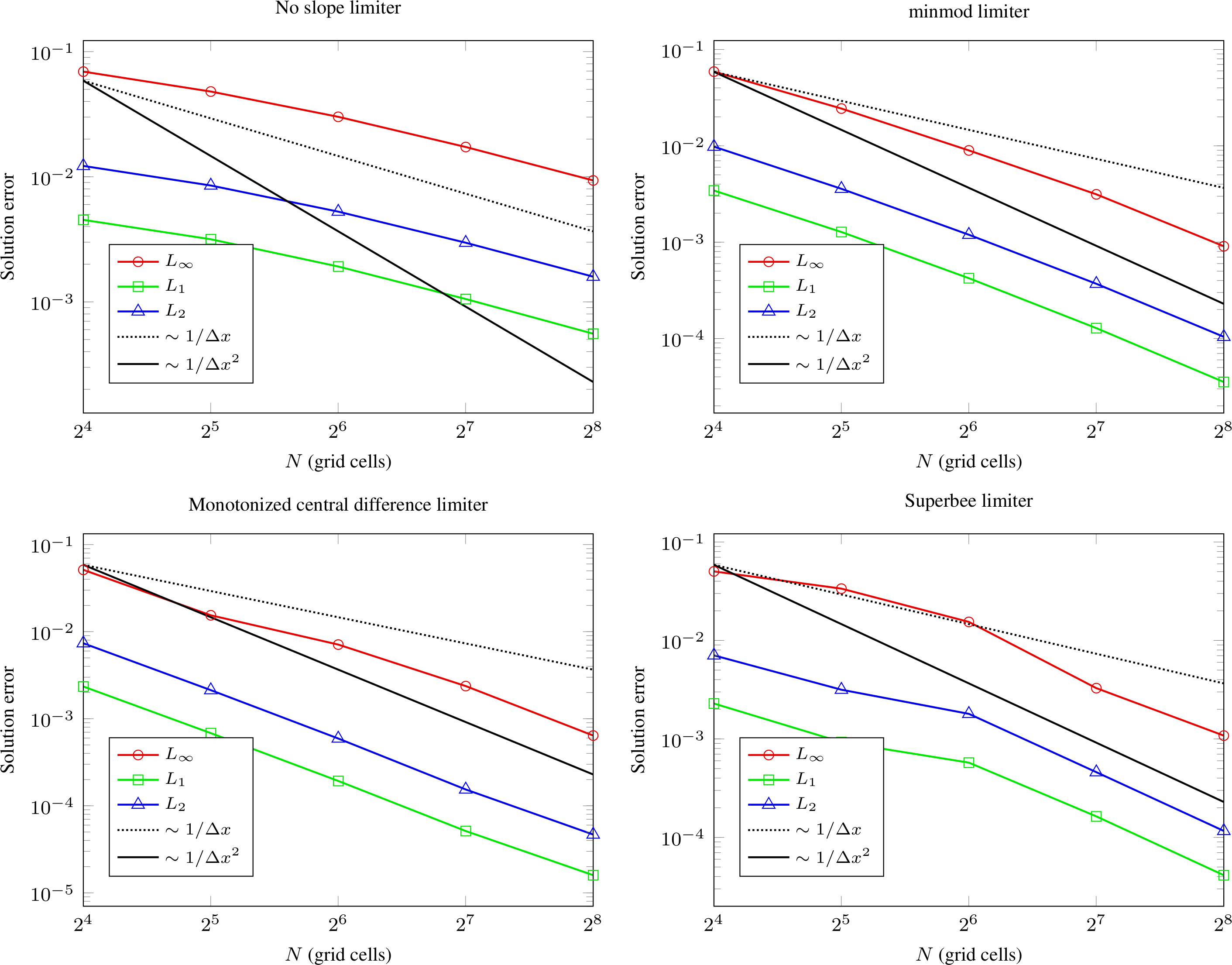
../_images/AdvectionDiffusionC1_2.png

Fig. 26 Spatial convergence rates with various limiters.

C2: Temporal convergence

A temporal convergence test is given in $DISCHARGE_HOME/Exec/Convergence/AdvectionDiffusion/C2. To compute the temporal convergence rate we compute two solutions using time steps \(\Delta t\) and \(\Delta t/2\), and estimate the solution error using the approach in Temporal convergence. Figure Fig. 27 shows the computed convergence rates for the second order Runge-Kutta and the IMEX discretization. As expected, we find 2nd order convergence for Heun’s method and first order convergence for the IMEX discretization.

../_images/AdvectionDiffusionC2.png

Fig. 27 Temporal convergence rates.